|
|
|
你拿披薩的方式,很可能是錯的 觀看數:1361 人

我們都遇到過這種情況。你抓起一塊披薩,正要一口吞掉的時候,披薩一下子軟了,從你的指尖處耷拉了下來。披薩餅本身的結構強度不夠高,無法支持整片的重量。也許下次應該少加點兒料?不用,無需絕望。
如果是是個吃披薩多年的老手,那你應該知道怎麼對付這樣的場景:隻需把披薩彎成U形即可。
| sponsored ads |
| sponsored ads |
(手頭沒有披薩?拿一張紙試驗一下就好。)

一張紙拿在手裡就會耷下去,但彎曲握就能讓它筆直。為什麼呢?
這個披薩小竅門的背後,深藏著一項關於曲面的強力數學。這一數學發現如此絕妙,以至於它的發明人——數學天才卡爾‧弗雷德里克‧高斯(Carl Friedrich Gauss)——給它起了個拉丁文名叫Theorema Egregium,意思是「絕妙定理」。
拿一張紙,捲成圓柱形紙筒。
| sponsored ads |
| sponsored ads |
你可能覺得顯而易見,紙本來是平的,捲成筒就彎了,對吧?可是高斯不這麼想。他想給紙的彎曲程度(「曲率」)下一個定義,讓它不因你人工施加的彎曲而改變。
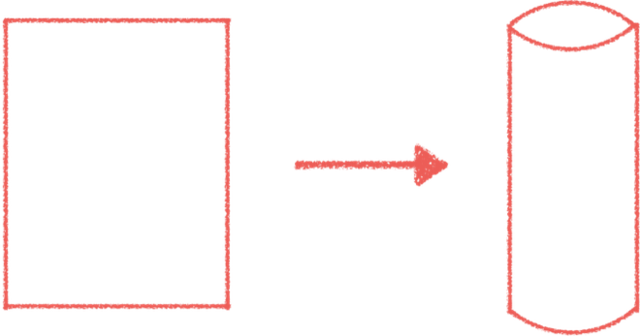
如果你放大去看一隻生活在紙筒上的螞蟻,這隻螞蟻可以走很多條不同的路線。它可以沿著彎曲道路橫著走下去,畫出一個圓;也可以沿著平坦路線豎著走,走出一條直線。或者它可以把兩種方式組合起來,走一條螺旋。
| sponsored ads |
| sponsored ads |
高斯的天才在於,他想到把所有這些路線都納入曲率定義裡面。辦法是這樣的:從任何一點出發,找到這隻螞蟻能選擇的最極端的兩條路線——也就是最凹的和最凸的兩條線。然後把它們的曲率乘起來。凸的路線曲率是正的,凹的路線曲率是負的,直的路線曲率是0。你得到的數字,就是那個點上的高斯曲率。
| sponsored ads |
| sponsored ads |

舉幾個例子吧。對於紙筒上的螞蟻來說,最極端的兩條路,一條是橫著畫圓,另一條就是豎著畫直線。但是因為直線具有0曲率,所以乘起來總是得到0。照數學家的說法,紙筒是平的——它的高斯曲率就是0。這正是因為你能用平整的紙張捲出一個紙筒。
| sponsored ads |
| sponsored ads |
相反,如果螞蟻活在一個球上,那麼它就無法找到平坦的路線,每一條道路都會有一定程度的向外凸出,所以高斯曲率一定是個正的數。所以,球是彎的,而筒是平的。你可以把一張紙捲成一個筒,卻永遠不能捲成一個球。

高斯的絕妙定理就是:生活在曲面上的螞蟻,根本不需要離開它就能知道曲面的曲率。隻要測量一下距離,計算一下就行。順便說,這也是為什麼我們沒有離開宇宙卻能測量出我們的宇宙是不是平的(根據目前的觀測來看,它是)。
但這個定理還有一個絕妙的結果:你可以隨意彎曲一個曲面,隻要你不拉長、壓縮或者撕裂它,高斯曲率一定不會變。因為單純彎曲不改變其上的距離,所以不管怎麼彎,上面的螞蟻總會計算出同樣的高斯曲率。
聽起來可能有點兒抽象,但是這推論有十分緊貼現實的結果。把一個橘子切成兩半,吃掉裡面的東西,然後把剩下半個橘子皮放在地上,踩吧。皮永遠不可能被踩扁成一個完整的圓。相反,它一定會裂開。這是因為球面和平面擁有不同的高斯曲率,所以不扭曲、不撕裂,是不可能把球面壓平的。有沒有試過給人寄籃球當禮物?包裝紙會遇到完全一樣的問題。不管你怎麼彎曲一張紙,它總會留下一點點「平」的痕跡,所以最後隻能得到皺皺巴巴一團糟。

橘子皮不可能壓成完整圓——因為球面和平面高斯曲率不同(而且橘子皮也沒有什麼延展性)。
這個定理的另一個推論是,平面紙上永遠不可能畫出準確的地圖。很多常見世界地圖投影方式能精確地保留角度,但是在面積上就有嚴重誤差。數學博物館的推特指出,服裝設計師也面臨類似挑戰——他們在平面上設計花樣,卻要符合彎曲的人體。
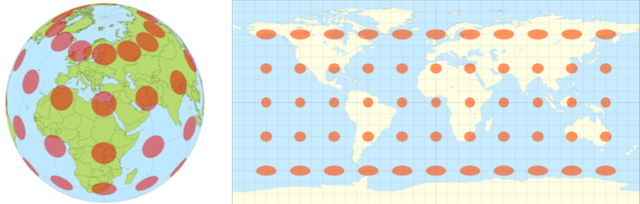
每個紅色圓圈的實際面積是相等的,但在地圖上看起來就有很大的差異。圖片來源:Stefan Kühn (左), Eric
那這一切和披薩餅有什麼關係呀?是這樣的:你拿起披薩之前,它是平的(數學上說,它的高斯曲率為0)。高斯絕妙定理指出,這片披薩必須有至少一個方向永遠保持平整——不管你怎麼彎,它一定會留下一點「平」的痕跡。當這片披薩塌下去的時候,平的方向(紅色箭頭)是朝側面的,這對吃掉它可沒有什麼幫助。但是如果你搶在它塌下去之前,先把披薩側著捏彎,就迫使另一個方向隻能保持平整——也就是對著你嘴巴的方向。還真是絕妙的定理呀。

沒想到幾何學也能這麼美味吧。
在一個方向上彎曲,來迫使它在另一個方向上保持平直。一旦你理解了這個點子,你就會到處都看到它。仔細看看一片草葉。它通常都是沿著中央葉脈彎曲的,這能幫助它維持筆直,不會軟塌下去。工程師經常用彎曲來強化結構承載力。在馬德里紮祖拉體育場,西班牙結構工程師埃杜拉多‧托羅亞(Eduardo Torroja)設計了一套創新的混凝土屋頂,從邊緣一直伸到看台上方,遮蔽了大片區域,而厚度隻有幾釐米。這其實就是披薩技巧。

彎曲的草葉。

西班牙紮祖拉體育場。圖片來源:Ximo Michavila
彎曲帶來力量。想想看:你能站在一個空易拉罐上,它能輕鬆承載你的體重;可是易拉罐外壁的厚度差不多和紙一樣薄。它的秘密就是它的彎曲。如果有人趁你站在上面的時候拿筆戳一下易拉罐,就能戲劇化地展現這一點——隻需一個小凹坑,它就會在你腳下轟然崩塌。

紙板箱裡隱藏的秘密。圖片來源:Craig Sunter / Flickr
但最日常的例子可能是無處不在的波形建材。世界上簡直沒有比紙板箱更無聊的東西,但是撕開一個這樣的箱子,你會看到箱壁裡一條熟悉的波浪曲線。這些皺褶在裡面可不是為了好看,它們是一種天才的結構方式:讓材料又薄又輕,又能堅硬到足以承擔可觀的重壓。

很多人小時候玩過的把戲:把一張紙摺疊幾次就能承載很大的重量,但它背後的數學可能你就想不到了。
波形金屬板使用的也是同樣的原理。這些不起眼的建材是純實用性的體現,它們的形態和其功能完美契合;它們的高強度和相對低廉造價使其成為了整個現代世界的背景。
今天,我們就算看到這些波浪形金屬板也幾乎不會多想什麼。但當它們誕生時,許多人把波形建材看成是奇蹟材料。1829年,亨利‧帕爾默(Henry Palmer)獲得了波形建材的專利,他是一個英國工程師,負責建造倫敦碼頭。帕爾默建起了世界上第一個波形鋼結構建築——倫敦碼頭的鬆油棚屋。雖然它今天看來可能沒什麼了不起,但是聽聽當時的一家建築學雜誌是怎麼描述它的吧:
不久前路過倫敦碼頭時,我們十分滿意地發現,帕爾默先生新發明的屋頂已經得到了實際應用。……任何一個目光敏銳的人,路過的時候都不可能不被它的優雅和簡潔所打動(雖然它隻是個棚屋);而隻要稍加思索,他們就會相信這一建築的效率之高、經濟之節約。我們認為,這是自亞當誕生以來,人類之手所建造的最輕又最結實(以其重量而言)的屋頂。若我們仔細觀察(我們為了這一目的而爬過了各式各樣的粘稠鬆油罐),會發現這一屋頂的總厚度絕對沒有超過十分之一英吋!
這年頭的建築學雜誌真是大不如前了啊。
雖然波形建材和易拉罐的強度可以很高,但有個辦法讓這些材料變得更強。想自己找到這個辦法?去冰箱拿個雞蛋出來。放在掌心,整隻手握住雞蛋,擠吧。(嘗試這個的時候記得別戴戒指。)你會為它的強度而驚訝的。我就沒法把雞蛋握壞,哪怕用盡全力也沒戲。(真的,誰試誰知道。)

請務必在家中嘗試一下——好吧,為了安全,別在電腦前嘗試。
雞蛋為什麼這麼強?易拉罐和波形金屬板在一個方向上是彎的,另一個還是平的。這一彎曲讓它們擁有了一定強度,但它們還是有可能被壓成本來的平板。
相反,雞蛋殼兩個方向上都是彎的。這是它的關鍵。用數學語言表達,那就是這些雙重彎曲的曲面擁有非零的高斯曲率。像我們先前遇到的橘子皮一樣,這意味著它們不可能被壓平,除非有撕裂或者拉伸——有高斯絕妙定理保證這一點。要打破一個雞蛋,你必須首先弄出一個坑。等到雞蛋失去了彎曲,也就失去了強度。
 核電站冷卻塔的象徵性形狀也在兩個方向上利用了彎曲。這個形狀叫做雙曲面,能讓所需的材料最少。正常的煙囪很像巨大易拉罐——結實是結實,但是很容易彎。雙曲面形狀的煙囪靠雙向彎曲來解決這個問題,這樣的彎曲方式能把形狀「鎖死」在空間中,提供額外的強度。
核電站冷卻塔的象徵性形狀也在兩個方向上利用了彎曲。這個形狀叫做雙曲面,能讓所需的材料最少。正常的煙囪很像巨大易拉罐——結實是結實,但是很容易彎。雙曲面形狀的煙囪靠雙向彎曲來解決這個問題,這樣的彎曲方式能把形狀「鎖死」在空間中,提供額外的強度。
另一種得益於彎曲的形狀是品客「薯片」,照數學家的說法,這是個雙曲拋物面(hyperbolic paraboloid,舌頭打結了沒?)。

自然界運用這一形狀的招數堪稱腦洞大開。瀨尿蝦有一項臭名昭著的本領——動物界裡最快的拳擊手,它的一拳打出去的力道足以把著力點上的水蒸發掉,創造出衝擊波和閃光。要想使出這死亡一擊,瀨尿蝦使用了雙曲拋物面形狀的「彈簧」。平時它把彈簧壓縮起來儲存巨大的能量,然後一招之內釋放出來。
西班牙-墨西哥建築師菲利克斯‧坎德拉(Félix Candela)很懂薯片形狀的力量。坎德拉是托羅亞的學生,他的建築將雙曲拋物面帶到了新的高度(字面意思)。當你聽到「混凝土」這個詞的時候,恐怕隻會想到無聊透頂的方塊建築,但坎德拉卻利用雙曲拋物面蓋起了巨大的建築,使用的混凝土薄到不可思議。身為這一材料的真正大師,他既是極富創新的建築者,也是結構藝術家。

所以為什麼薯片形狀強度如此之高?這和它平衡張力與壓力的方式有關。一切建築都要支撐重量,最終將這些重量傳遞到地面上。這一傳遞可以靠兩種不同方式完成:其一是壓縮,拱頂就是純靠壓力而實現的例子;另一個就是拉伸,把一根鎖鏈拎起來,它的每一環就都處於拉伸狀態、受到張力。雙曲拋物面結合了兩種方式的優點。凹下去的U型部分處於拉伸狀態,而凸起來的拱頂部分則是壓縮,高斯絕妙定理則保證了任何一個地方的受力都會傳遞到四周——因為這是一個高斯曲率非零的曲面。隻要你試圖改變它的形狀,就必須得連帶壓縮或者拉伸一整片區域才能讓結果遵從高斯的律令;像紙張那樣隻彎曲一條線而不影響其他部分是不可能的。通過這樣的雙重彎曲,這一形狀實現了張力和壓力之間的精妙平衡,讓它以很小的厚度就能實現驚人的強度。
通過彎曲來產生強度,這個想法塑造了我們所見的當代世界,而它的根源卻來自萬古不變的幾何學。所以下一次你抓起一塊披薩的時候,記得朝周圍看看,欣賞一下這個簡單的披薩小把戲背後的龐大遺產吧。
來源
這裡滾動定格